
30 May - 01 June
Technical
TECH TUESDAY: What Monza wing levels tell us about the performance of Red Bull, Ferrari and Mercedes

Share

Mark Hughes explains the different rear wing choices used by Red Bull, Ferrari and Mercedes at Monza – and what those parts tell us about the characteristics of each car, as Giorgio Piola provides technical illustrations.
The rear wing choices of the top three teams at Monza – the track which has the most lap time sensitivity to straight-line speed – reflected very clearly the big spread in aerodynamic efficiency between their cars.
It confirmed in a much more emphatic way the indications suggested from other tracks this year – which is that the Red Bull clearly has the most efficient aerodynamics and the Mercedes the least. With Ferrari somewhere in between.
READ MORE: The 3 key factors that enabled Verstappen to win the Italian Grand Prix
All four power unit suppliers are adamant that from their analysis of GPS traces, there is a tiny spread in performance between the strongest and weakest. Therefore, any differences we see at Monza are a reflection of the respective drag of the three main cars.
But the drag of the cars is also a function of the amount of rear wing each team decides to use. The more efficient a car’s downforce, the more rear wing area it can justify.

Verstappen passing Russell's Mercedes for P2
Downforce always induces drag, but the optimum compromise between the two will vary from track to track and car to car. Aerodynamic efficiency can be expressed as how much extra drag each increment of extra downforce induces. Or how much downforce is lost for each increment of drag reduction.
F1 NATION: Max’s maiden Monza win and debut delight for De Vries – it’s our Italian GP review
Monza’s elongated layout obviously rewards low drag more than any other circuit, and hence everyone is running their car with skinny wings relative to other tracks. But for two equally low-drag cars, the one with more downforce should still lap faster. Downforce is still rewarded, just not by as much as usual.
Red Bull’s Monza rear wing had more surface area than either of their rivals. Its mainplane was dished, in contrast to those of the Ferrari and Mercedes – which were completely flat. Although the RB18 mainplane was much smaller than usual, its dished contours would ensure a bigger pressure differential between its upper and lower surfaces, and therefore more downforce – and drag.
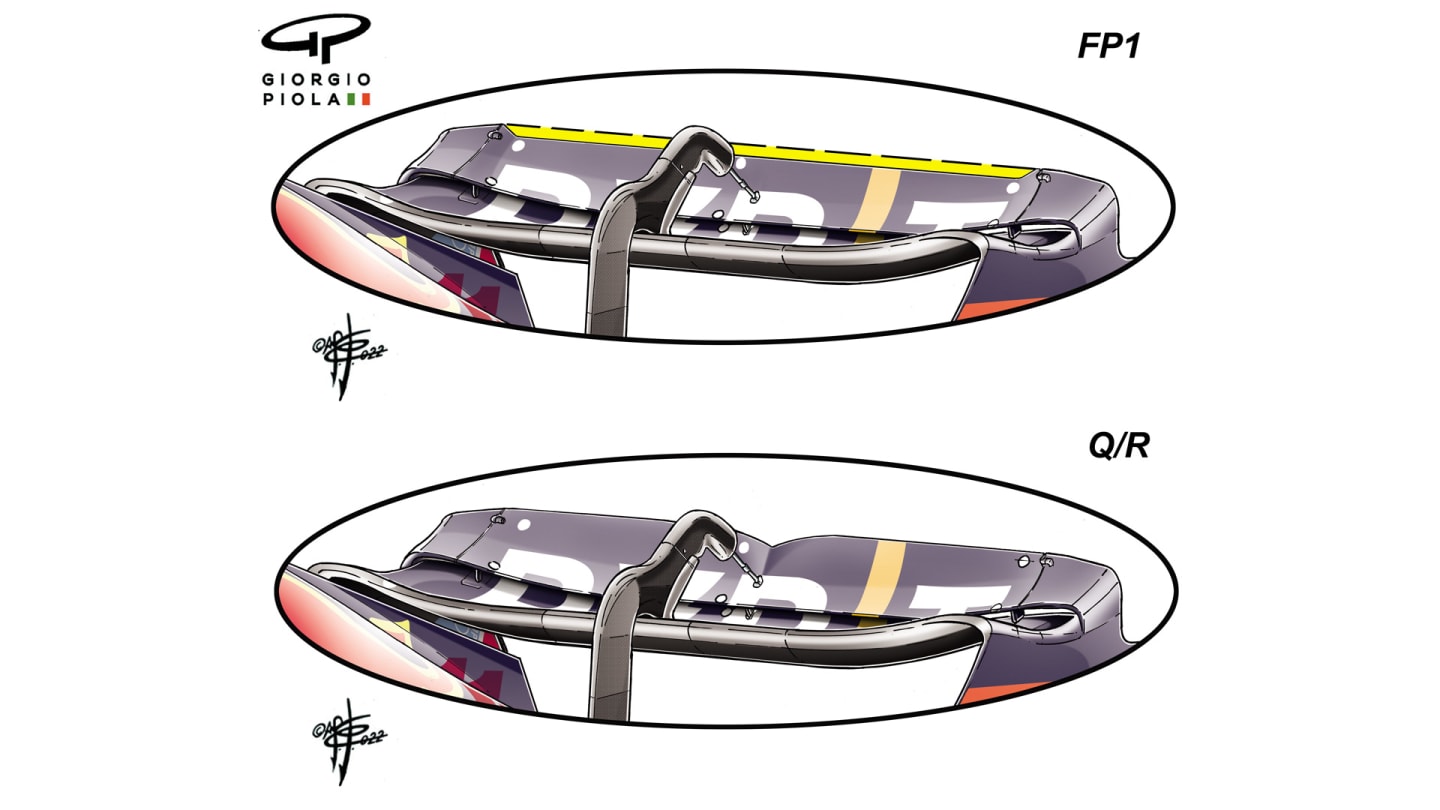
Red Bull ran with the bigger of their available flaps after trying a cut-back version in FP1. Although the main plane is quite small, the flap is run at quite an aggressive angle, helping to create good downforce. The RB18’s aero efficiency allowed this wing setting to be competitive, helping minimise tyre deg.
Red Bull's upper flap was also run at quite an aggressive, more downforce-inducing, angle. The team tried a cut-back version of the flap in FP1 but ran subsequently with the fuller version. They also retained a twin-flap beam wing. The beam wing, by training the air onto the underside of the main wing, increases downforce (and drag).
The RB18’s aerodynamic efficiency allowed it to be as fast as the Ferrari and faster than the Mercedes on the straights despite carrying more wing.
Ferrari had a tiny and flat mainplane, a single flap beam wing and less flap area than Red Bull, but more than Mercedes. Although comparable in straight-line performance to the Red Bull, the Ferrari lacked that car’s downforce through the Lesmos and Ascari.

Ferrari sported a tiny flat mainplane, more flap area than Mercedes – but less than Red Bull.
Mercedes were trimming as much drag from their car as they possibly could, costing them a lot of downforce.
They ran an extremely trimmed-back flap, a single beam wing and that very flat mainplane. For qualifying and the race they even removed the gurney flap on the trailing edge of the flap. Despite all that, Mercedes were the slowest of the trio on the straights and over a lap.
As F1 returns to tracks that are less drag-sensitive, the differences in aero efficiency between the cars will likely give a smaller performance difference over the lap than was evident at Monza.
1 / 2
YOU MIGHT ALSO LIKE
News Tsunoda gives verdict on Gasly collision as he admits he needed to ‘qualify better’ in Monaco
News ‘It’s not how we want to go racing’ – Albon rues frustrating ‘tactical game’ in Monaco
News Wolff reveals Williams boss Vowles sent him an apology text during Monaco GP
Feature F1 FANTASY: Strategist Selection – What’s the best line-up for the 2025 Spanish Grand Prix?









)
